Stephan Paukner :: syslog :: Entries from Wednesday, April 18. 2007

Wednesday, April 18. 2007

Electric guitar string gauge calculation

I currently wonder what string gauge (diameter) I should use for my electric guitar. The standard is .009 (i.e. 0.009″ for the high e-string). Thinner strings allow easier string bending, but one has to play with less finger pressure to avoid detuning. As I like to tune all strings down by one halftone, the strings get even “softer”. So one should take a higher string gauge when tuning down. The question is now: Do downtuned .010’ers correspond to normally tuned .009’ers? What gauge should one use when one wants to tune down e.g. by a whole tone and have the “softness” of .009’ers? Here’s my try of a calculation:

Does a downtune by one octave correspond to a loss of half the tension? Whatever amount the tension will get, it doesn’t decrease linearly with the halftones—remember the different distances between the frets! How does one calculate this scale? You can’t just divide the half of the string length by 12 to get the steps between the frets.

Calculating the fret stepping of a guitar
For the 12th halftone, you arrive at ½ of the string length, for the 24th halftone you arrive at ¼ of the length, etc.; the 12th divides the length by 2, the 24th divides it by 4, the 36th divides it by 8, etc. Abbreviating d(n) for the divisior at halftone n, we have d(0)=1, d(12)=2, d(24)=4, d(36)=8, etc., i.e. d(12n)=2ⁿ and therefore d(n)=2^n/12. For the n-th halftone, the string length becomes

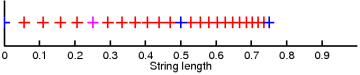
$\displaystyle L_n := \frac{L}{d(n)} = \frac{L}{2^{n/12}} = \frac{L}{\sqrt[12]{2^n}}$ .

If you don’t believe my derivation, maybe you believe a (modified) function plot:

n=0:24; dv=1./(2.^(n/12)); plot([1-dv 1], ones(1, length(dv)+1), ’+r’) hold; plot(1-dv(0+1), 1, ’+b’) %zeroth fret plot(1-dv(12+1), 1, ’+b’) %first octave plot(1-dv(24+1), 1, ’+b’) %second octave plot(1-dv(5+1), 1, ’+m’) %fifth fret

The blue crosses indicate the first two octaves, occurring when ½ (=50%) and ¾ (=75%) of the length are removed. The pink cross indicates the fifth fret at about ¼ (=25.085%) of the length. Every guitarist should recognize the fret stepping here!

Gauge stepping when tuning down
I found a link which explains that the relation between string diameter δ, tension t and frequency f is

$\displaystyle \delta = C\frac{\sqrt{t}}{fL}$ ,

where C is a constant depending on the material. The aforementioned scaling is still valid for the frequencies, i.e., when the frequency f is tuned down by n halftones, the resulting frequency f_n is given as

$\displaystyle f_n = \frac{f}{\sqrt[12]{2^n}}$ ,

what can be verified for f=440Hz: The next lower tunes are 415.3Hz (n=1) and 392Hz (n=2), and the next higher tunes are 466.2Hz (n=−1) and 493.9Hz (n=−2). Replacing f by f_n in the previous equation yields that when the tension is to be kept, one has to take strings with diameter $\delta_n = \delta\cdot\sqrt[12]{2^n}$ . As example, .009’er strings that are tuned down by one whole tone should be replaced by .010’ers to keep the tension of the .009’ers.

The other way round, fixing δ_n=0.010 (the taken string gauge) and δ=0.009 (the desired string gauge “feel”), one derives

$\displaystyle n = \log_2 \left( \frac{\delta_n}{\delta} \right)^{12}$

what results in n=1.82 in this example, a downtune of slightly less than a whole tone. Tuning down .010’ers a “complete” whole tone corresponds to a string gauge of .0089’ers, so really almost .009’ers.

As a final rule of thumb, the steps between the string gauges correspond to tune changes of a whole tone. The following table shows how certain string gauges “feel” when they are tuned down:

tuning	.008	.009	.0095	.010	.011	.012	.013
E♭	.0076	.0085	.009	.0094	.0104	.0113	.0123
D	.0071	.008	.0085	.0089	.0098	.0107	.0116
D♭	.0067	.0076	.008	.0084	.0092	.010	.011
C	.0063	.0071	.0075	.0079	.0087	.0095	.0103
B	.006	.0067	.0071	.0075	.0082	.009	.0097