Stephan Paukner :: syslog

Entries from Sunday, April 9. 2006

Sunday, April 9. 2006

Inclusions of $L^p$-spaces

Master's Thesis
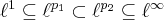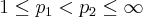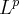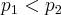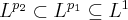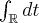Just a note: We know that the inclusion \ell^1\subseteq\ell^{p_1}\subset\ell^{p_2}\subseteq\ell^\infty yields for 1\leq p_1<p_2\leq\infty. A similar inclusion statement is valid for L^p-spaces iff we look at L^p[a,b]. Here, for p_1<p_2, the inclusion is the other way round: L^{p_2}\subset L^{p_1}\subseteq L^1. This is not valid for L^p(\mathbb{R}), as \int_{\mathbb{R}}dt is not finite. In Cigler’s script, the fact 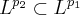L^{p_2}\subset L^{p_1} had just been written down quickly, and it wasn’t mentioned that this was only valid for bounded intervals. I already wondered why it was always said that the Fourier transform could be expanded to “L^2\cap L^1” and not simply “L^2”.
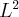Posted by Stephan Paukner in Master's Thesis at 18:30 | Comments (0) | Trackbacks (0)
Defined tags for this entry:
(Page 1 of 1, totaling 1 entries)

Calendar

Back April '06 Forward
Mon Tue Wed Thu Fri Sat Sun
          1 2
3 4 5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23
24 25 26 27 28 29 30

Quicksearch

Archives

Categories

Show tagged entries

Syndicate This Blog

Follow me

XING LinkedIn QRZ Diigo GitHub
Google Maps contributions YouTube Vimeo Likes Goodreads

Bookmarks

(More)

Powered by