Inclusions of $L^p$-spaces

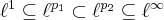
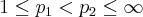
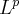
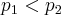
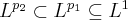
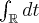
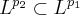
Just a note: We know that the inclusion yields for . A similar inclusion statement is valid for -spaces iff we look at . Here, for , the inclusion is the other way round: . This is not valid for , as is not finite. In Cigler’s script, the fact had just been written down quickly, and it wasn’t mentioned that this was only valid for bounded intervals. I already wondered why it was always said that the Fourier transform could be expanded to “” and not simply “”.
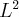