Entries tagged as octave
Related tags
guitar mathematics matlab music review automobile bash bug german image processing literature fun history podcast privateMonday, March 12. 2007
Time-frequency shifts of a 2D-Gaussian

The modulated Gaussian I showed previously was just illustratory and did not consider mathematical properties such as FT-invariance. For that, it has to be periodized, normalized and centered at the borders. The MATLAB script gaussnk.m by N. Kaiblinger from the NuHAG toolbox implements this by evaluating the Gauss function on a wider interval and then wrapping it into the desired signal length. I tried to do that for the 2D case, but here I’m not sure about the term “signal length”, it should actually be the number of pixels. I wrote a first gauss2.m which creates a 2D-Gaussian on a square with almost all desired properties. However, the normalization seems to be wrong, as it does not fulfill ,
and
as desired. I have to become familiar with the discrete definition, I don’t know how the norming factors come up; maybe they consider the dimension d as a power.
What I was trying to do was doing localized FFT2’s on a test image. I shifted an arbitrarily selected Gaussian like a spotlight aver an image and did FFT2’s of that. However, on white walls the result didn’t show the desired FT-invariance of the Gaussian. So I had to think of the aforementioned normalizing tasks. Then I was confused that shifts of a Gaussian actually result in modulations on the FT-side. But shouldn’t we want to stay the FT all the same while shifting the Gaussian over a white wall in the input image (and having an unchanged Gaussian at every spot)? Yes, but only as long as we don’t want to be able to invert the FT! Here, we’d need the modulations to get back to the corresponding shifts on the input image. So, if only the spectra are interesting, one should look at the absolute values of the FT which will make the modulation factors disappear (because they have an absolute value of 1).
Another thing I came over was this; look at the following example image: On the left half is the input, and the right half shows the absolute values of the FFT2. The input almost looks like a modulated Gaussian. Why doesn’t it simply shift on the output image? Because in the input, the black values of the surroundings match the black values of the line pattern! If the input should represent a modulated Gaussian, the black lines should have value -1, and the surroundings a gray level of 0. I’ll correct this soon.


I like to rotate the output by 90° to match the orientation of the shifts with that of the lines in the input. Notice that I shifted the mid tones in the output image and that I always get another Gaussian in the center. This is the one I have to get rid of. Also, I get some kind of symmetry, the cause of which I haven’t found out yet but might also be due to the scaling issue.
For that, I visualized the TF- and FT-behavior of my 2D-Gaussian:
Continue reading "Time-frequency shifts of a 2D-Gaussian"
Wednesday, November 15. 2006
The exponential in $R^d$, II

(Q15) I’m gonna show you some cool Gabor atoms on .
, as described previously, indeed looks like this:


See how the value of the frequency changes with the length of , and the direction with the orientation of
, just as described previously.
In the STFT, these frequencies get reduced locally by an “envelope function”. One could take the Gaussian window to achieve this:


And now these are the modulated Gaussians, whose set of translates across forms the building blocks for Gabor analysis on
:


Sunday, November 12. 2006
The exponential in $R^d$

In question 15 I want to make a picture how looks like for
. I want to take at least two-dimensional vectors, as the inner product is too trivial otherwise. But then
is a function on
, which is rather difficult to plot. So I want to fix
and plot
, which is then a function on
with values in
and therefore easy to plot. As the inner product is
, it is in the 2-dimensional case a simple plane-equation
; of course, the inner product is linear and goes through the origin! It cuts the zero-plane
in an angle which is dependent on the orientation of the fixed
: The zero-line evolves where the vectors
are orthogonal to the fixed
, i.e.,
.
This zero-line will now change its angle on the zero-plane while varying the fixed vector . This gives a picture how it behaves as a whole. In Octave, I set
[xx yy]=meshgrid(linspace(-2,2,50));
and then made a plot corresponding to by
mesh(xx+yy)
The resulting 3D-plot shows a boring inclined plane. To better see the location and orientation of the zero-line, I plot the absolute values:
mesh(abs(xx+yy))
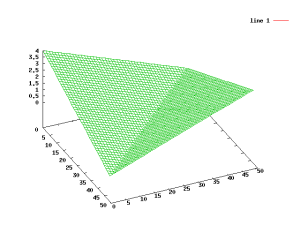
To see the orientation even better, I chose
imagesc(abs(xx+yy))
imagesc(abs(xx+2*yy))
imagesc(abs(-xx+4*yy))
corresponding to the further vectors and
. This is what I get:



The turning around of that plane now corresponds to the behavior of the mentioned inner product function on . (Beware that the absolute values used in the plots hide the asymmetry of the inner product function!) The values are always real and go into the exponent of the exponential function.
then “rotates fastest” as
runs along to a fixed
, and is constant = 1 if it runs orthogonally; Beware that there’s a difference whether it is constant = 1 or if it reaches that value again and again. So, in the integral of the FT, the exponential function simply covers all frequencies via exhausting all values of
, and the FT is then a function in
, which takes out a single orientation of those frequencies; As already mentioned some time ago, the term “frequency” isn’t useful anymore in higher dimensions. For two-dimensional signals, i.e. images, a “frequency” can be interpreted as a pattern of lines: The narrower the pattern, the higher the frequency is. The difference to one-dimensional signals is, that those frequencies may now have an angle. It is not enough to just look at a single frequency of that line-pattern, but also to all their orientations! Only with using all orientations of patterns, an image can be analyzed according to the contained frequencies. The 2D-FT of an image therefore tells you what patterns occur in what orientation. To be more precise, you select the frequency by the length
and the orientation by its angle
, because the inner product as a function in
grows faster with growing length of
. For me, this is now a milestone in understanding the 2D-FT.
About
Calendar
| Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|
| ← Back | February '26 | |||||
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | |