Entries tagged as mathematics
Wednesday, May 30. 2007
Separable vs. non-separable lattices

I used P. Prinz’ toolbox to compute a 2D dual atom on a separable lattice and on a quincunx lattice. It shows that even if both lattices have same redundancy, the dual might be better localized on the quincunx lattice:
In this example, the norm difference of the “quincunx dual” to the original is about 0.1, and that between the “separable dual” and the original is almost 1.0. To achieve more similarity on the separable lattice, one has to take a higher redundancy.
I’m still not sure what the term “separability” actually expresses for 4D lattices: There exist position lattices (on the image space), frequency lattices (on the FT space), and TF-lattices (for both dimensions). If the atom is separable into its two dimensions, then one can compute the two 1D duals and obtain the 2D dual from their tensor product. If one takes two quincunxes for computing those two 1D duals, does this correspond to a non-separable 4D PF-lattice? In the case of 1D signals, a separable TF-lattice means that there’s always the same set of frequencies taken at every position. A quincunx lattice means that there are two different sets of frequencies chosen alternately while walking along the position points. Maybe the same interpretation works for the 2D case. I haven’t analyzed Prinz’ routine yet, but I think that he takes a rectangular (separable) frequency lattice and shifts it alternately by a half of the lattice-point distance while walking along the position spots. Should one try to use a quincunx position lattice? Well, I’ll have to experminent with that.
HGFei asked me to contact Søndergaard, because that topic of non-separability is currently not only “hot” for myself.
Friday, May 25. 2007
Dilated + rotated 2D Gaussian

I’ve finally improved my script that computes a dilated and rotated 2D Gaussian with respect to low memory consumption. It applies a dilation and rotation matrix to the 2D domain. I published it under the GNU GPLv2, so if you find any improvements, you are forced to share them. ![]()
I still have the impression that it is rather slow, but I currently don’t know how to do it better. Of course, it has to be evaluated on
% Computes a non-separable (dilated + rotated) 2D Gaussian
% Usage: g = nsgauss(p, q, vdil, hdil, rot);
% Input: p,q .... size of g
% vdil ... vertical dilation factor (before rotation)
% hdil ... horizontal dilation factor (before rotation)
% rot .... rotation angle, e.g. pi/4
% Example:
% norm(nsgauss(p,q,1,1,0) - gaussnk(p)’*gaussnk(q)) == eps
%
% Version 0.2-20070525
% by Stephan Paukner {stephan+math at paukner dot cc}
% Licensed under the GNU General Public License v2
% $Id: nsgauss.m,v 1.2 2007/05/25 10:14:52 ps Exp ps $
D=[1/vdil 0; 0 1/hdil]; %dilation matrix
R=[cos(rot) -sin(rot); sin(rot) cos(rot)]’; %’%rotation matrix
sp=sqrt(p); sq=sqrt(q);
g=zeros(1,p*q);
for jp=-3:3
for jq=-3:3
[x y]=meshgrid( (0:p-1)/sp + jp*sp , (0:q-1)/sq + jq*sq );
v=D*R*[x(:)’; y(:)’];
g=g+exp(-pi*(v(1,:).^2 + v(2,:).^2));
end
end
g=reshape(g,q,p)’; %’
g=g/norm(g,’fro’);
Here’s a comparison of computing time and accuracy:
And some plots using different parameters:
 |  |
 |  |
 |  |
Monday, May 21. 2007
2D dual via 1D dual

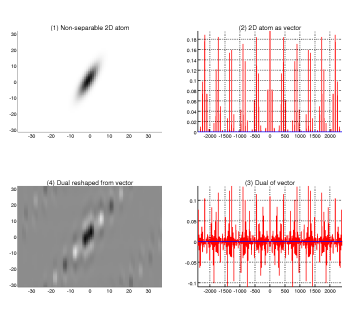
Yesterday I finally wrote a routine which computes a non-separable (dilated and rotated) 2D Gaussian. It takes parameters for horizontal and vertical dilation of the 2D Gaussian which is then rotated by a corresponding parameter. If it is neither dilated nor rotated, it is numerically identical to the pure 2D Gaussian. It has
With this I could finally reproduce a graphic from the paper “2D-GA Based on 1D Algorithms”: It shows (1) a non-separable 2D atom with relatively prime height and width, (2) the atom mapped to vector shape, (3) the dual of that vector with regard to some combined time and frequency steps, and (4) the dual vector reshaped to an image.
The question remains about how to finally do GA using these two 2D atoms. The only ways I found so far was either building the 1D Gabor system (of the atom shaped as vector) or computing a sampled STFT by that 1D vector; this works because modulations stay modulations. However, in the case of separable 2D atoms, this can be done in another way, as I’ll show in another article.
About
Calendar
| Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|
| ← Back | January '26 | |||||
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |