I think I found out where the mentioned property comes from: The solution lies in the application of a substitution in the mentioned integral. It is well known that a translation of any (Lebesgue integrable) function leads to a modulation of its Fourier transform, i.e., 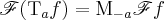 , where
, where 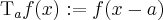 and
and 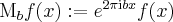 for
for 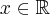 . But, it is even a common property for any
. But, it is even a common property for any 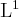 -function
-function 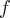 that
that 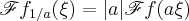 , where we again use the symbolism
, where we again use the symbolism 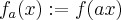 . This becomes clear by using the substitution
. This becomes clear by using the substitution 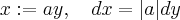 :
:
So, it’s clear ( ) that this means
) that this means 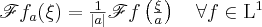 , and not only for the Gaussian function
, and not only for the Gaussian function 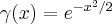 . And, for
. And, for 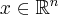 , the substitution
, the substitution 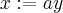 leads to
leads to 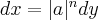 , because if
, because if 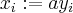 , then
, then 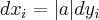 and therefore
and therefore 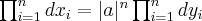 . I’ll have to recall what the “value of the functional determinant” is.
. I’ll have to recall what the “value of the functional determinant” is.
Regarding the proof that the Gaussian function is an eigenfunction of the Fourier transform, HGFei once handed us one out which seems to be more elegant than the proofs which use the well definedness of solutions for initial value problems of linear common differential equations.