Functions with compact support

Tuesday, March 14. 2006

Functions with compact support

I finished chapter IV on friday and continued on Hilbert space theory. Unfortunately, when it came to connections with Fourier transformation (Sobolev and Schwartz spaces, distributions), my understanding began to slow down. Some questions occured:

Why is $\langle f^\prime,\varphi\rangle=-\langle f,\varphi^\prime\rangle$ for $\Omega\subset\mathbb{R}^n, \, f\in\mathrm{C}^1(\Omega)$ and $\varphi\in\mathscr{D}(\Omega)$ , i.e., why is

$\displaystyle\int_\Omega\, f^\prime(x)\overline{\varphi(x)}\,dx=-\int_\Omega\, f(x)\overline{\varphi^\prime(x)}\,dx$

for $\varphi$ with compact support? Why do the border terms in the partial integration disappear in this case?
What’s so special about functions with compact support anyway?

Any literature I seeked just had written that fact down without justifying it, as if it were so simply to see. And finally, I saw it: The confusion I had was that I misinterpreted 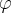$\varphi$ as being 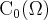$\mathrm{C}_0(\Omega)$ only, i.e., disappearing at infinity (The closure of $\{x\in\Omega\quad:\quad\varphi(x)\geq\varepsilon\}$ is compact). Here, it definitely was not clear that its values already disappear before infinity.

The rule of partial integration says, 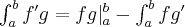$\textstyle\int_a^b f^\prime g = fg|_a^b - \int_a^b fg^\prime$ , where 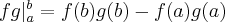$fg|_a^b = f(b)g(b)-f(a)g(a)$ . If the integration should go over the whole space, then 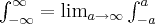$\textstyle\int_{-\infty}^\infty = \lim_{a\to\infty}\int_{-a}^a$ , and the same is with $fg|_{-\infty}^\infty$ .

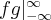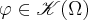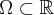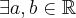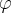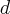Now, if $\varphi\in\mathscr{K}(\Omega)$ with $\Omega\subset\mathbb{R}$ being an interval, it follows that $\exists a,b\in\mathbb{R}$ where $\varphi$ already disappers, because it has compact (and therefore bounded) support; $(a,b)\supset[c,d]$ , where $c$ and $d$ are the left and right borders of 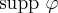$\operatorname{supp}\,\varphi$ . And this is why 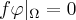$f\varphi|_\Omega=0$ in the first question above.

For the sake of completeness, it is clear by the following what 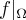$f|_\Omega$ should mean for $\Omega\subset\mathbb{R}^n$ :

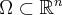$\displaystyle\int_{[a,b]\times[c,d]}f(x,y) \,d(x,y) =$

$\begin{eqnarray*}\displaystyle\quad &=& \int_c^d\int_a^b f(x,y)\,dx\,dy\\ &=& F(x,y)|_{x=a}^{x=b}|_{y=c}^{y=d}\\ &=& \left(F(b,y)-F(a,y)\right)_{y=c}^{y=d}\\ &=& F(b,d)-F(b,c)-F(a,d)+F(a,c)\end{eqnarray*}$

Posted by Stephan Paukner in Master's Thesis at 08:54 | Comments (0) | Trackbacks (0)

Defined tags for this entry: mathematics

Trackbacks

Trackback specific URI for this entry

No Trackbacks

Comments

Display comments as (Linear | Threaded)

No comments

Add Comment

Name
Email
Homepage
In reply to
Comment	Phone* What is one plus four? Enclosing asterisks marks text as bold (word), underscore are made via _word_. Standard emoticons like :-) and ;-) are converted to images. To prevent automated Bots from commentspamming, please enter the string you see in the image below in the appropriate input box. Your comment will only be submitted if the strings match. Please ensure that your browser supports and accepts cookies, or your comment cannot be verified correctly. Enter the string from the spam-prevention image above: BBCode format allowed
	Remember Information? Subscribe to this entry
Submitted comments will be subject to moderation before being displayed.