d-dimensional Fourier transform

Wednesday, February 1. 2006

d-dimensional Fourier transform

I know what the factor $e^{2\pi\mathrm{i}x\omega}$ for $x,\omega\in\mathbb{R}$ in the definition of the Fourier transform

$\displaystyle(\mathscr{F}f)(\omega) = \int_{\mathbb{R}} f(x)e^{-2\pi\mathrm{i}x\omega}\,dx$

means, if that factor is seen as a function in $x$ : If $\omega$ is fixed, then the variation of $x$ delivers the circle function, returning to the starting point for every $x\omega\in\mathbb{N}$ .

But what if $x,\omega\in\mathbb{R}^d$ ? Here, $x\cdot\omega$ has to be understood as the inner product $\langle x,\omega\rangle$ and the integral turns into the $d$ -dimensional Lebesgue-integral, i.e., if $x=(x_1,\ldots, x_d)$ , this means

$\displaystyle\int_{\mathbb{R}^d}dx = \int_{-\infty}^{\infty}\cdots\int_{-\infty}^{\infty}dx_1\cdots dx_d$

Now, what has to be understood by $e^{2\pi\mathrm{i}\langle x,\omega\rangle}$ in higher dimensions?

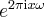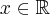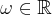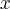Let’s see what $e^{2\pi\mathrm{i}x\omega}$ as a function in $x\in\mathbb{R}$ does for a fixed $\omega\in\mathbb{R}$ : The larger $\omega$ gets, the “faster” the circle function rotates, i.e., the frequency rises. The integral happens for such a fixed value of $\omega$ along the $x$ -axis. In two dimensions, it doesn’t make sense anymore to talk about time and frequency, as the signal does not “evolve in time”, but on a plane, i.e., it could be interpreted as a picture. Higher dimensions could only have a physical interpretation, like energy and location probability. In addition, it is not clear anymore what to understand by a 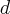$d$ -dimensional frequency.

Another point is to understand a product 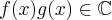$f(x)g(x)\in\mathbb{C}$ , whereas it is quite easy to understand it in 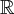$\mathbb{R}$ : In the latter, the product function “gets reduced to those places, where both functions have non-zero values”, so to say. Where one function has zero value, the product has zero value, too, and where both have “large” values, the product becomes an “even higher value”. But how is this to understand in the complex plane? Here, if a function has complex values, its graph is a path in the complex plane (if it is continuous). What does the graph of the product function look like? This is not easy to understand anymore for higher dimensions.

I have to think more about why the Fourier transform is an indicator of “how much” the frequency $\omega$ occurs in 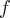$f$ .

Posted by Stephan Paukner in Master's Thesis at 08:39 | Comments (0) | Trackbacks (0)

Defined tags for this entry: mathematics

Trackbacks

Trackback specific URI for this entry

No Trackbacks

Comments

Display comments as (Linear | Threaded)

No comments

Add Comment

Name

Homepage

Comment

In reply to

Phone*

What is three plus seven?

Enclosing asterisks marks text as bold (*word*), underscore are made via _word_.

Standard emoticons like :-) and ;-) are converted to images.

To prevent automated Bots from commentspamming, please enter the string you see in the image below in the appropriate input box. Your comment will only be submitted if the strings match. Please ensure that your browser supports and accepts cookies, or your comment cannot be verified correctly.
CAPTCHA