Sunday, January 11. 2009
Magic ball volumes in high-dimensional spaces

Currently I’m dealing with the topic of machine learning at work, and I stepped over the so-called curse of dimensionality, where the volume of the unit ball (radius=1) becomes negligible compared to the volume of the unit cube (side length=1) which is always equal to 1, what yields problems when selecting a number of training samples in a (very) high-dimensional feature space. My team-mate and I stepped over an interesting thing concerning the volume of the unit ball in higher dimensions.
First of all, the formula for calculating the volume of the ball Brn ⊂ ℝn with radius r is given as
.
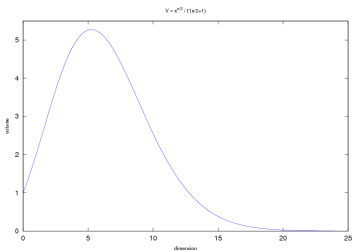
In two dimensions (n=2) we get the volume as the well-known circle area r2π, and as Γ(2.5)=¾√π, we get the ball volume for n=3 as 4⁄3r3π. In higher dimensions the resulting formula isn’t that simple anymore, but we’re only interested in the numerical values anyway. We now restrict to r=1. Following one’s intuition, the volume increases with the dimensions (ball volume is larger than circle area), but see what happens beginning with n=5 and n=13:
| n | V | n | V |
|---|---|---|---|
| 1 | 2 | 11 | 1.88 |
| 2 | π ≈ 3.14 | 12 | 1.34 |
| 3 | 4⁄3π ≈ 4.19 | 13 | 0.91 |
| 4 | 4.93 | 14 | 0.60 |
| 5 | 5.26 | 15 | 0.38 |
| 6 | 5.17 | 16 | 0.24 |
| 7 | 4.72 | 17 | 0.14 |
| 8 | 4.06 | 18 | 0.08 |
| 9 | 3.30 | 19 | 0.05 |
| 10 | 2.55 | 20 | 0.03 |
This is indeed interesting: The ball volume starts to decrease and even goes to zero in higher dimensions, although its radius is always 1! What does that mean? And why is the unit cube able to keep its volume of 1, although it seems to be contained within the unit ball? Another thing we see: A bit past n=5 the function reaches its maximum of something a bit larger than 5. Do we have V(x0)=x0 for x0=sup V(x)? And if so, what’s its value?
The key in understanding this issue lies in the corners of the unit cube: Their distance to the origin goes to infinity with increasing number of dimensions! For the unit square (2-cube), their distance is √½ ≈ 0.71, and for the 3-cube it’s already √¾ ≈ 0.87. At n=4 their distance is √1=1 and thus the corners already touch the unit ball. In higher dimensions the unit cube is not completely contained within the unit ball anymore, but still its volume is constant =1 and the nearest points of the sides remain at a distance of ½!
Regarding the question about where the maximum of the volume formula is reached, I noticed that I’d need to do advanced numerical derivations whose knowledge I lack.
About
Calendar
| Mon | Tue | Wed | Thu | Fri | Sat | Sun |
|---|---|---|---|---|---|---|
| ← Back | January '09 | Forward → | ||||
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |