Master's Thesis

Tuesday, April 3. 2007

Images to vectors and back

Regarding the previous questions I noticed that GA on LCA groups is too general for my concerns and that the study of GA on finite abelian groups is enough.

In a certain paper HGFei published a result that for p×q-images where p and q are relatively prime there is an isomorphism to a vector of length N=pq. The theory considers the groups $\bbZ_p\times\bbZ_q$ and $\bbZ_N$ where $\bbZ_k:=\bbZ/k\bbZ$ . One explicit mapping from the matrix indices $\left(\begin{smallmatrix}j\\ k\end{smallmatrix}\right)$ to the corresponding vector indices is given by

$\iota\colon \bbZ_p\times\bbZ_q \to \bbZ_N, \quad \left(\begin{matrix}j\\ k\end{matrix}\right) \mapsto \beta qj + \alpha pk \pmod N$

where α and β are integers chosen such that

$\alpha p+\beta q \equiv 1 \pmod N$ .

My 480×480 zebra-image doesn’t have a height and width that are relatively prime, so I simply drop one pixel of height:

> im=img(2:480,:); > size(im) ans = 479 480 > gcd(479,480) ans = 1

Just for a first test I set α=p and β=q and define a primitive mapping function. (I’ll have to find a quicker transform, as in my tests the switching takes too long. But this could be due to the actually large test image. In addition, I currently only manage to do the backward step by storing the indices in an index matrix.)

> function ii=ma2ve(j,k) > p=479; q=480; a=p; b=q; > ii = mod(b*q*j+a*p*k , p*q); > if ii==0; ii=p*q; end > endfunction > ma2ve(1,1) ans = 1 > ma2ve(1,2) ans = 229442 > p*q ans = 229920

I have to return N instead of 0 to have a correct index value. Although the mapping is actually an isomorphism I didn’t know how to go back to the tuple (j,k), so I store the indices in an index matrix while building the image vector:

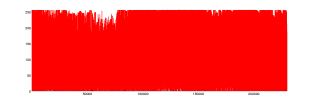
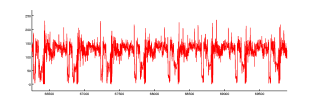
> idx=zeros(p,q); imv=zeros(1,N); > tic; for ii=1:p; for jj=1:q; > idx(ii,jj) = ma2ve(ii,jj); > imv(idx(ii,jj)) = im(ii,jj); > end; end; toc Elapsed time is 58.358711 seconds.

58 seconds!? However, the image looks like this as a vector: