Thursday, March 15. 2007
Convolving a zebra with modulated Gaussians
I finally managed to scale the reconstructed images appropriately such that one can see at what locations certain 2D-frequencies occur. I FT’ed an image of a zebra and “windowed” the FT with a shifted Gaussian. Doing the inverse FT of that cutout yields a convolution of the input image with a modulated Gaussian, corresponding to
This is the zebra, a 480×480 pixel sample I clipped from an image I found in the Wikimedia Commons, and its FFT2:
Again, I rotated the image of the FT by 90° to match the orientation of the “jets” with the line patterns in the zebra. Clearly, the vertically oriented frequencies dominate the image. Now I window the FT-image by placing a Gaussian at the origin. This results in a low-pass filter. The IFT gives a reconstructed image which only contains the lowest frequencies:
The left half shows the (unmodulated) Gaussian with which the original image has been convolved. The right half shows the reconstructed image—the animal has lost all its zebra patterns! This effect is identical to a Gaussian blur.
I wrote a script which shifts the Gaussian along a spiral on the FT-image, starting at the origin. This means increasing the value of the frequency while rotating. For each step I reconstructed the image. I created more than 1,300 images which I rendered to a video. Here are some highlights:
In this sample there’s a response at the lower neck of the animal.
Here the low vertical frequencies, such as legs and tail, have almost vanished because of the low horizontal modulation. Again there’s a high response at the lower neck of the zebra.
Again the neck, here better visible, and already a little response at the body.
Nice response at the upper hind limbs and the head. The legs and tail are actually invisible.
The long awaited high response at the body.
Nice response at the upper fore limbs.
Finally, some responses to higher frequencies at the head.
For your viewing pleasure, I also provide the complete video:
I won’t publish the M-script that created these images, as it’s still too basic, but above all it incorporates some scripts from the NuHAG toolbox anyway.
Categories
Follow me
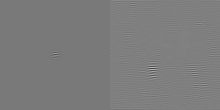
Logbook of Stephan Paukner on : Images to vectors and back