Convolutions

(Q26) Meanwhile, I know that a convolution of one function 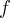$f$ with another function 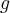$g$ means that 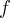$f$ will be “ 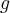$g$ -smeared”, and vice versa. I visualized some convolutions using Octave. I was prepared to implement 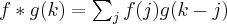$f*g(k)=\sum_jf(j)g(k-j)$ for two vectors, but then stepped over HGFei’s conv2fei which makes the surprising use of the identity 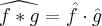$\widehat{f*g}=\hat f\cdot\hat g$ ; I wouldn’t have come to the idea to do it this way, you only have to multiply two FFT’s and then do the inverse FFT.

First I convolved a square with a small Gaussian—this is nothing less than a Gaussian blur:

$*$

$=$

Note that the blur would already occur even if the second object were solid! Look at the square convolved with itself:

$*$

$=$

Then I watched how these bars convolve with each other:

	$*$		$=$
	$*$		$=$

Notice how the blurness shrinks when the two objects can’t overlap much.

Posted by Stephan Paukner in Master's Thesis at 16:48 | Comments (0) | Trackback (1)

Defined tags for this entry: mathematics

Trackbacks

Trackback specific URI for this entry

Logbook of Stephan Paukner on : Convolving a zebra with modulated Gaussians

I finally managed to scale the reconstructed images appropriately such that one can see at what locations certain 2D-frequencies occur. I FT&#8217;ed an image of a zebra and &#8220;windowed&#8221; the FT with a shifted Gaussian. Doing the inverse FT of th

Comments

Display comments as (Linear | Threaded)

No comments

Add Comment

Name

Homepage

Comment

In reply to

Phone*

What is one plus six?

Enclosing asterisks marks text as bold (*word*), underscore are made via _word_.

Standard emoticons like :-) and ;-) are converted to images.

To prevent automated Bots from commentspamming, please enter the string you see in the image below in the appropriate input box. Your comment will only be submitted if the strings match. Please ensure that your browser supports and accepts cookies, or your comment cannot be verified correctly.
CAPTCHA